Prerequisite:
Please study below topics before starting current tutorial.
2. Stack
4. Recursion
5. DFS
Why traversal algorithm is required?
- The purpose of the tree or graph is to organize the collection of data in the graph or tree format based on problem requirement. But to process the data represented in the tree or graph data structure, some mechanism is required. These set of mechanisms are called traversal algorithms and such traversal is required to process data represented by the tree or graph.
Definition:
Postorder traversal is a type of depth-first traversal used in binary trees which starts from root node and process all the nodes of the tree. In postorder traversal, the nodes are recursively visited and processed in the following order:
- Traverse the left subtree in postorder- First go to the left child node if it is present, apply the postorder traversal on the left child node.
- Traverse the right subtree in postorder. - Once the left subtree has been processed, go to the right child node and apply postorder traversal on the right child node.
- Process data at current node- Once postorder has been applied on the left child node and the right child node, process the data stored in the current node( In starting it is root node).
In short we can memorize this algorithm as LEFT-->RIGHT-->ROOT or in short LRRt formula. It means, first apply postorder on the left subtree of given root/current node then apply postorder traversal on the right subtree of given root/current node then at last process the data present at root/current node. For reference, in remaining tutorial we will recall this formula in short as LRRt.
Example - How Postorder traversal works :
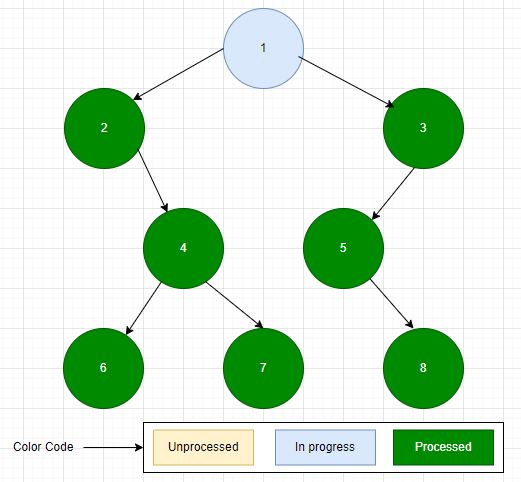
First we concentrate on the below binary tree to understand the postorder binary tree traversal:
1. Since node 1 is the root node here, processing will start from node 1.
3. Node 2 doesn't have any left subtree so according to LRRt formula postorder traversal is applied on the right subtree of node 2 which starts from node 4. Node 4 has a left subtree so postorder traversal is applied on the left subtree of node 4 as given below:
6. Node 7 is leaf node so according to LRRt formula LR part is processed as it has no left and right subtrees. The last part Rt means data at node 7 is processed. Since it is the last part of LRRt, node 7 is completely processed and control backtracks to node 4.
7. Now the left and right subtrees of node 4 has been processed so the last part of formula LRRt is remaining that is Rt. So data at node 4 is processed. Since Rt is the last step in LRRt, node 4 is also processed and control backtracks to node 2.
8. LR part at node 2 is processed so last part Rt(data at current node) is also processed. And accordingly node 2 is also processed and control backtracks to node 1.
9. According to LRRt formula only L part(the left subtree) has been processed and RRt is remaining. So next step will be the processing of the right subtree of node 1 which is rooted on node 3. Node 3 has left subtree rooted at node 5 so postorder traversal is applied on node 5. Again node 5 doesn't have left subtree so next postorder traversal is applied on its right subtree which is rooted on node 8.
11. Since node 5 has no left subtree and its right subtree has been processed to the last part Rt(data at current node) is processed. Since Rt is the last step, node 5 is completely processed and control backtracks to node 3 where as mentioned above node 3 is also processed and control backtracks to node 1.
12. LR part at node 1 has been processed so remaining part Rt(data at current node) is also processed. Since Rt was the last step in formula LRRt node 1 is also processed which is the root node. So whole tree is processed here.
Output of the the above postorder traversal will be : 6,7,4,2,8,5,3,1
Implementation:
To represent the tree node, below data structure will be used in this tutorial.
Postorder traversal can be implemented by two methods.
Method 1: Using STACK
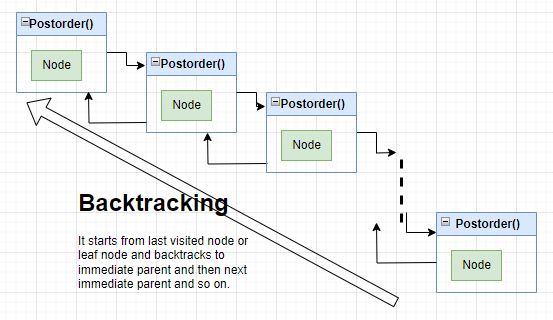
In postorder traversal it can be easily observed that a node is only processed if LRRt formula is fully applied on the given node. Fully means if node has left subtree then it must be processed, then the same for right subtree. If left subtree has another left or right subtree then those subtrees must be processed. This process will go till the leaf node then backtracking happens from there.
Remember till backtracking a chain of partial processed nodes exist where it is necessary to keep track of order of vertices in which Postorder traversal algorithm has been applied on the partial processed nodes. The first full processing happens on the last node(leaf node) then process returns back to the node which is predecessor of the last visited node and so on.
Here we see that a chain of partial processed nodes is created where backtracking happens or the first full processing happens on the last added node in the chain. After that this node is removed from the chain. And the root node is completely removed from the chain at last. If we try to remember such data structure where last added node is processed first and first added node is processed last then such type of data structure is LIFO(Last In First Out) which is STACK data structure. Below figure illustrates the same.
postorderByStack(root)
{
- Let ST1 and ST2 are two stacks
- ST1.push(root)
- While ST1 is not empty:
- {
-
item=ST1.pop()
-
if item.left is not null then ST1.push(item.left)
-
if item.right is not null then ST1.push(item.right)
-
ST2.push(item)
- }
- While ST2 is not empty:
- {
-
current=ST2.pop()
-
Process current.data(print current.data)
- }
Below is the explanation of the above algorithm:
- root node is pushed on stack ST1 in the starting.
- Stack ST1 completes the LR part of formula LRRt iteratively using while loop present at line no 3. In this loop left node is pushed first then right node.
- While popping stack ST1 at line no 5 always pushed right node comes first which is again pushed to stack ST2. That's why stack ST2 stores result in LIFO( Last In First Out) order.
- To get final result ST2 is popped one by one(First pushed record here means the last element in the postorder traversal and vice versa).
Method 2: Using Recursion
From the above figure we can easily see postorder traversal can be implemented recursively. As we know from Recursion chapter, while designing recursive solution there are 3 steps to follow which are given below:
Hypothesis - In designing recursive solution we should define a function and its necessary parameters which will solve the given problem. In our case while applying postorder traversal to any node we need the left child, node data and the right child node which will be accessed from the given node itself. So only the current node is sufficient input parameter where processing will start from the root node. We are defining below function which will solve our problem.
Postorder(root)
Inductive Step - Here we need to define the problem in terms of the subproblems of itself. Here we know from the above mentioned formula postorder works on formula LRRt(Apply postorder on the left subtree,apply postorder on the right subtree, process the data on current node ). So we can define postorder traversal as below in the inductive step.
Postorder(root)=Postorder(root.left)==>Postorder(root.right)==>(process data at root)
or
Postorder(root)=
Postorder(root.left)
Postorder(root.right)
(Process data at root)
Base Condition - Function body defined in the Inductive step will not work as after leaf node left or right child will be null so there must be some condition to handle this boundary which is called Base Condition. Here if current node is null means no subtree to process. So there must not be any processing when the current node is null as given below:
Postorder(root)=
if root is null do nothing and return
Postorder(root.left)
Postorder(root.right)
(Process data at root)
So below will be postorder tree traversal algorithm for a given binary tree using recursion
postorderByRecursion(root)
{
{
- If the root node is null then do nothing and return
- Postorder(root.left)
- Postorder(root.right)
- Process root.data(print root.data)
Below is the java code implementation for the above mentioned Postorder tree traversal algorithms
import java.util.Stack;
public class PostorderTraversalTest {
/**
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
Node n1=new Node(1);
Node n2=new Node(2);
Node n3=new Node(3);
Node n4=new Node(4);
Node n5=new Node(5);
Node n6=new Node(6);
Node n7=new Node(7);
Node n8=new Node(8);
n1.left=n2;
n1.right=n3;
n2.right=n4;
n3.left=n5;
n4.left=n6;
n4.right=n7;
n5.right=n8;
System.out.println("===============Below is Postorder By Stack===============");
PostorderTraversal order=new PostorderTraversal();
order.inorderByStack(n1);
System.out.println("===============Below is Postorder By Recursion===============");
order.inorderByRecursion(n1);
}
}
class Node
{
int data;
Node left;
Node right;
public Node(int k)
{
data=k;
}
}
class PostorderTraversal
{
public void inorderByStack(Node root)
{
Stack<Node> st1=new Stack<Node>();
Stack<Node> st2=new Stack<Node>();
st1.push(root);
while(!st1.isEmpty())
{
Node item=st1.pop();
if(item.left!=null)
{
st1.push(item.left);
}
if(item.right!=null)
{
st1.push(item.right);
}
st2.push(item);
}
while(!st2.isEmpty())
{
Node item=st2.pop();
System.out.println(item.data);
}
}
public void inorderByRecursion(Node root)
{
if(root==null)
{
return;
}
inorderByRecursion(root.left);
inorderByRecursion(root.right);
System.out.println(root.data);
}
}