Motivation:
In real life there are scenarios where collection of data share many to many relationship among them. To represent such type of data and relationship among them, Graph data structure is used. For example a network of cities connected to each other.
Definition:
A graph is a user defined, non liner data structure used to represent data and relationship among them.
It consists a set of nodes (also called vertices) and a set of edges that connect pairs of nodes. Graphs are used to represent various kinds of relationships and structures in computing, including networks, paths, and hierarchies.
Graph is represented as G(N,E) where N is set of nodes and E is set of edges. For above example we can logically define graph as below:
G(N,E) is a graph where N={city1,city2,city3,city4,city5} and E={e13,e14,e15,e23,e25,e34,e45}
Components of a Graph
- Vertices (Nodes): These are the individual elements or points in the graph. For example - In a social media network, each person would be treated as a vertex.
- Edges: These are the connections between the vertices. For example In the social media network, an edge would represent a friendship or connection between two people.
Types of Graphs
-
Undirected Graph: The edges have no direction. If there is an edge between vertices A and B, you can traverse from A to B and from B to A.
-
Directed Graph (Digraph): The edges have a direction. If there is a directed edge from vertex A to vertex B, you can traverse from A to B, but not necessarily from B to A.
-
Weighted Graph: Each edge has a weight or cost associated with it. This is common in scenarios like road networks where distances or travel times are represented as weights.
- Unweighted Graph: The edges do not have weights. The connections are simple and uniform.
Representations of Graphs
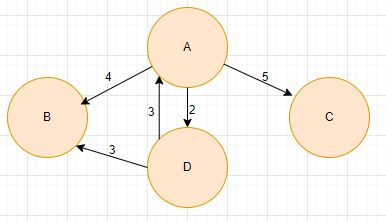
To understand representation of a graph we are taking below example:
-
Adjacency Matrix: A 2D array where the cell at row i and column j represents the presence (if weighted graph then weight) of an edge between vertices i and j. For above example we assume Vertexes A,B,C and D are treated as indexes 0,1,2 and 3. Then their graph representation of above diagram will be:
-
Adjacency List: An array or list where each element represents a vertex and contains a list of below objects .
- List of vertices if graph is not weighted graph.
- List of vertex and weight pair(vertex, edge weight from given vertex) if graph is not weighted graph.
Below is the representation of the graph mentioned in the above example:
A->{(B,4),(C,5),(D,2)}
D->{(A,3),(B,3)}
Below is the java code implementation of the above mentioned graph representations
package graph;
import java.util.ArrayList;
import java.util.Hashtable;
import java.util.List;
public class GraphRepresentationTest {
/**
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
GraphRepresentation g=new GraphRepresentation();
g.adjacencyMatrix();
g.adjacencyList();
}
}
class GraphRepresentation
{
public void adjacencyMatrix()
{
//Integer.MAX_VALUE is used here to represent infinity (Means no link between two vertices)
char [] vertices={'A','B','C','D'};
int[][] graph={
{0,4,5,2}
,{Integer.MAX_VALUE,0,Integer.MAX_VALUE,Integer.MAX_VALUE}
,{Integer.MAX_VALUE,Integer.MAX_VALUE,0,Integer.MAX_VALUE}
,{3,3,Integer.MAX_VALUE,0}
};
System.out.println("===========================Adjacency Matrix Representation===========================");
for(int i=0;i<4;i++)
{
for(int j=0;j<4;j++)
{
if(i!=j&&graph[i][j]!=Integer.MAX_VALUE)
{
System.out.println("Edge:"+vertices[i]+"->"+vertices[j]+"="+graph[i][j]);
}
}
}
}
public void adjacencyList()
{
char [] vertices={'A','B','C','D'};
Hashtable<Integer,List<int[]>> graph=new Hashtable<Integer, List<int[]>>();
List<int[]>children=new ArrayList<int[]>();
children.add(new int[]{1,4});
children.add(new int[]{2,5});
children.add(new int[]{3,2});
graph.put(0, children);//Adding vertex A and its children
children=new ArrayList<int[]>();
children.add(new int[]{0,3});
children.add(new int[]{1,3});
graph.put(3, children);//Adding vertex D and its children
System.out.println("===========================Adjacency List Representation===========================");
for (int key : graph.keySet()) {
for(int[] item:graph.get(key))
{
System.out.println("Edge:"+vertices[key]+"->"+vertices[item[0]]+"="+item[1]);
}
}
}
}
Common Graph Algorithms
- Depth-First Search (DFS): An algorithm for traversing or searching tree or graph data structures. It starts at the root (or an arbitrary node) and explores as far as possible along each branch before backtracking.
- Breadth-First Search (BFS): An algorithm for traversing or searching tree or graph data structures. It starts at the tree root (or an arbitrary node of a graph) and explores the neighbor nodes at the present depth prior to moving on to nodes at the next depth level.
- Dijkstra's Algorithm: An algorithm for finding the shortest paths between nodes in a graph, which may represent, for example, road networks.
- Bellman-Ford Algorithm: Computes shortest paths from a single source vertex to all of the other vertices in a weighted digraph. It is slower than Dijkstra's algorithm but more versatile, as it is capable of handling graphs in which some of the edge weights are negative numbers.
- Kruskal's Algorithm: An algorithm for finding the minimum spanning tree (MST) for a connected weighted graph.
- Prim's Algorithm: Another algorithm for finding the minimum spanning tree (MST) for a connected weighted graph.
Graphs are fundamental in various fields, such as computer science, biology, transportation, social sciences, and more, due to their ability to model relationships and structures efficiently.